\( \vec{C_P}=\vec{C} - \frac{\vec{A} \times (\vec{CB}\times \vec{A})}{{|\vec{A}|}^2} =\vec{C} - \frac{(\vec{A} \times \vec{CB})\times \vec{A}}{{|\vec{A}|}^2} \) (In 2D and 3D only) ...(2)
where \(\vec{CB}=\vec{C}-\vec{B}\), \(\vec{C_P}\)=Position Vector of Projected Point \(C_P\)
The Projection of Origin on the Line (i.e. when Position Vector \(\vec{C}=\vec{0}\) or NULL Vector ) is given by \(\vec{C_P}=\vec{B_\perp}\).
where \(\vec{CB}=\vec{C}-\vec{B}\), \(\vec{C_P}\)=Position Vector of Projected Point \(C_P\)
The Projection of Origin on the Line / Plane / Hyperplane (i.e. when Position Vector \(\vec{C}=\vec{0}\) or NULL Vector ) is given by \(\vec{C_P}=\vec{B_{||}}\).
- In 2 Dimensions the Projection of a Point having Coordinates (\(x_c,y_c\)) on a Line having Coordinate Equation \(ax + by + c=0\) is given as:
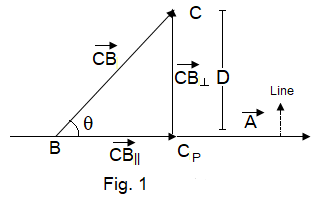
Equation Form Vector Form \(x_p = x_c - D \hat{a} \)
\(y_p = y_c - D \hat{b} \)\( \begin{bmatrix} x_p \\ y_p \end{bmatrix} = \begin{bmatrix} x_c \\ y_c \end{bmatrix} - D \begin{bmatrix} \hat{a} \\ \hat{b}\end{bmatrix} \) (\(\hat{a},\hat{b}\))=Unit Vectors corresponding to coefficients a and b of Line
\(D\)= Signed Distance from Point to Line=\(\frac{ax_c+by_c+c}{\sqrt{a^2+b^2}}\)
\((x_p,y_p)\)=Coordinates of the Projected Point - In 3 Dimensions the Projection of a Point having Coordinates (\(x_c,y_c,z_c\)) on a Plane having Coordinate Equation \(ax + by + cz +d =0\) is given as:
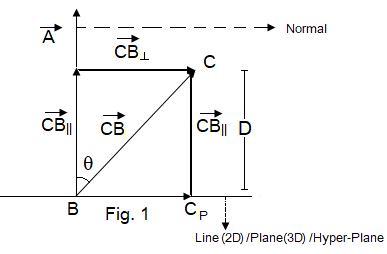
Equation Form Vector Form \(x_p = x_c - D \hat{a} \)
\(y_p = y_c - D \hat{b} \)
\(z_p = z_c - D \hat{c} \)\( \begin{bmatrix} x_p \\ y_p \\ z_p \end{bmatrix} = \begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} - D \begin{bmatrix} \hat{a} \\ \hat{b} \\ \hat{c} \end{bmatrix} \) (\(\hat{a},\hat{b},\hat{c}\))=Unit Vectors corresponding to coefficients a, b and c of Plane
\(D\)= Signed Distance from Point to Plane=\(\frac{ax_c+by_c + cz_c + d}{\sqrt{a^2+b^2+c^2}}\)
\((x_p,y_p,z_p)\)=Coordinates of the Projected Point - In any Arbirary N Dimensions (where \(N \geq 2\)) the Projection of a Point having Coordinates (\(x_{1c},x_{2c},x_{3c},\cdots,x_{nc}\)) on a Line / Plane / Hyper Plane having Coordinate Equation \(a_1x_1 + a_2x_2 + a_3x_3 + \cdots + a_nx_n + a_{n+1}=0\) is given as:
Equation Form Vector Form \(x_{1p} = x_{1c} - D \hat{a_1} \)
\(x_{2p} = x_{2c} - D \hat{a_2} \)
\(x_{3p} = x_{3c} - D \hat{a_3} \)
\(\vdots\)
\(x_{np} = x_{nc} - D \hat{a_n} \)
\( \begin{bmatrix} x_{1p} \\ x_{2p} \\ x_{3p} \\ \vdots \\ x_{np} \end{bmatrix} = \begin{bmatrix} x_{1c} \\ x_{2c} \\ x_{3c} \\ \vdots \\ x_{nc} \end{bmatrix} - D \begin{bmatrix} \hat{a_1} \\ \hat{a_2} \\ \hat{a_3} \\ \vdots \\ \hat{a_n} \end{bmatrix} \) (\(\hat{a_1},\hat{a_2},\hat{a_3},\cdots,\hat{a_n}\))=Unit Vectors corresponding to coefficients \(a_1\), \(a_2\), \(a_3\), \(\cdots\), \(a_n\) of Line / Plane / Hyper-Plane
\(D\)= Signed Distance from Point to Line / Plane / Hyperplane=\(\frac{a_1x_{1c}\hspace{1mm}+\hspace{1mm}a_2x_{2c}\hspace{1mm}+\hspace{1mm}a_3x_{3c}\hspace{1mm}+\hspace{1mm}\cdots\hspace{1mm}+\hspace{1mm}a_nx_{nc}\hspace{1mm}+\hspace{1mm}a_{n+1}}{\sqrt{{a_1}^2\hspace{1mm}+\hspace{1mm}{a_2}^2\hspace{1mm}+\hspace{1mm}{a_3}^2\hspace{1mm}+\hspace{1mm}\cdots\hspace{1mm}+\hspace{1mm}{a_n}^2}}\)
(\(x_{1p},x_{2p},x_{3p},\cdots,x_{np}\))=Coordinates of the Projected Point
- In 2 Dimensions the Projection of a Point having Coordinates (\(x_c,y_c\)) on a Line having Unit Normal form of Coordinate Equation \(ax + by + c=0\) where \(a\) and \(b\) are Components of Unit Vector Normal to the Line and \(c\) is the Signed Distance of the Line from Origin is given as
\(\begin{bmatrix} 1 - a^2 & -ab & -ac\\-ab & 1-b^2 & -bc\\0 & 0 & 1\end{bmatrix} \begin{bmatrix} x_c \\ y_c \\ 1\end{bmatrix} = \begin{bmatrix} x_p \\ y_p \\ 1\end{bmatrix}\)
where (\(x_p,y_p\)) are Coordinates of the Projected Point - In 3 Dimensions the Projection of a Point having Coordinates (\(x_c,y_c,z_c\)) on a Plane having Unit Normal form of Coordinate Equation \(ax + by + cz + d=0\) where \(a\), \(b\) and \(c\) are Components of Unit Vector Normal to the Plane and \(d\) is the Signed Distance of the Plane from Origin is given as
\(\begin{bmatrix} 1 - a^2 & -ab & -ac & -ad\\-ab & 1-b^2 & -bc & -bd\\-ac & -bc & 1-c^2 & -cd \\0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix} x_c \\ y_c \\z_c \\ 1\end{bmatrix} = \begin{bmatrix} x_p \\ y_p \\ z_p \\ 1\end{bmatrix}\)
where (\(x_p,y_p,z_p\)) are Coordinates of the Projected Point - In any Arbirary N Dimensions (where \(N \geq 2\)) the Projection of a Point having Coordinates (\(x_{1c},x_{2c},x_{3c},\cdots,x_{nc}\)) on a Line / Plane / Hyper-Plane having Unit Normal form of Coordinate Equation \(a_1x_1 + a_2x_2 + a_3x_3 + \cdots + a_nx_n + a_{n+1}=0\) where \(a_1\), \(a_2\), \(\cdots\), \(a_n\) are Components of Unit Vector Normal to the Line / Plane / Hyper-Plane and \(a_{n+1}\) is the Signed Distance of the Line / Plane / Hyper-Plane from Origin is given as
\(\begin{bmatrix} 1 - {a_1}^2 & -a_1a_2 & -a_1a_3 & \cdots & -a_1a_n & -a_1a_{n+1}\\-a_2a_1 & 1-{a_2}^2 & -a_2a_3 & \cdots & -a_2a_n & -a_2a_{n+1}\\-a_3a_1 & -a_3a_2 & 1-{a_3}^2 & \cdots & -a_3a_n & -a_3a_{n+1} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ -a_na_1 & -a_na_2 & -a_na_3 & \cdots & 1-{a_n}^2 & -a_na_{n+1} \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix} \begin{bmatrix} x_{1c} \\ x_{2c} \\ x_{3c} \\ \vdots \\ x_{nc} \\ 1\end{bmatrix} = \begin{bmatrix} x_{1p} \\ x_{2p} \\ x_{3p} \\ \vdots \\ x_{np} \\ 1\end{bmatrix}\)
where (\(x_{1p},x_{2p},x_{3p},\cdots,x_{np}\)) are Coordinates of the Projected Point